Trie 树

所有在老鼠岛上的老鼠都应该学习Trie树！——伟大的吱嘎鼠

Trie树，就是所有Oier们喜闻乐见的字符串的超级优化的数据结构！

已阅，狗屁不通。——吱嘎鼠

字典树，顾名思义，是一颗很像字典的树，将相同前缀的字符串合并在一起，当出现不同时就分支，成为这样的树。

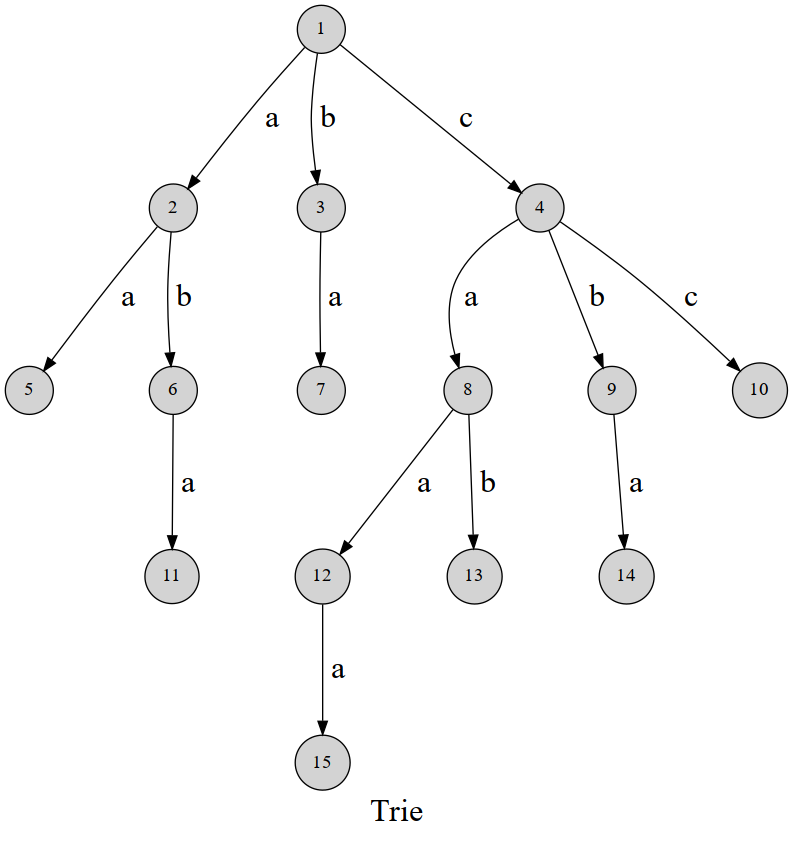
在这样的树上，我们可以很快地完成关于前缀的问题。

Master of Both 题面

先看题面~

Hui-Bot教授是弦论和高级数据结构的大师，所以他提出了一个有趣的问题。给定一个仅由小写英文字母组成的 \(n\) 字符串序列，当按字典顺序比较字符串时，该序列中有多少个反转？

作为Hui-Bot最出色的学生，普塔塔和布达达分别掌握了高超的弦理论和先进的数据结构技能，他们轻松地一起解决了这个问题。然而，存在 \(q\) 个不同的平行宇宙，其中字母表中的字符并不按原始顺序出现。

形式上，每个宇宙中的字母都是一个字符串，它是26小写英文字母的排列，表示每个字符出现的顺序。

当且仅当以下条件之一成立时，字符串 \(a\) 按字典顺序小于字符串 \(b\) ：

\(a\) 是 \(b\) 的前缀，但 \(a \ne b\) ；
在a和b不同的第一个位置，字符串a有一个字母在字母表中出现的时间早于b中对应的字母。
长度n的序列a中的反转次数是满足 $ 1 \le i \le j \le n$ 、 \(a_j < a_i\) 的有序对(i,j)的数量。

请帮助各个宇宙的普塔塔和布达达解决问题。

输入 $1 \le n \le 5 \cdot 10^5 $ , $ 1 \le q \le 5 \cdot 10^4 $

\(1 \le \lvert s_i \rvert \le 10^6\) \(\lvert si \rvert\) 的总和不大于 \(10 ^ 6\)

鼠的思路

这道题要看的是字符串，一个一个比较过去复杂度岂不是会爆炸awa
所以将所有对都记录下来，看看其他时间的单词表里这个对是不是逆序的，用字典树预处理就好啦！

ll trie[N][37], cnt = 0, sm[N], rel[37][37];
void insert(string s){
	int p = 0;
	for(auto c : s){
		int u = c - 'a' + 1;//为什么要 + 1，那当然是因为有的坏字符串是别的字符串的前缀，所以要在后面加一个比 $a$ 字典序都小的东西
		if(!trie[p][u]) trie[p][u] = ++cnt;
		for(int j = 0; j <= 26; j++){//看看自己的“同事”，记录对
			if(j == u)continue;
			rel[j][u] += sm[trie[p][j]];//有时候一个点会挤着很多字符串
		}
		sm[p = trie[p][u]] ++;//锵锵，统计一下
	}
}

接下来就是要统计了

while(q--){
		string s; cin >> s;
		ll ret = 0;
		for(int i = 0; i < 26; i++){
			ret += rel[s[i] - 'a' + 1][0];
			for(int j = 0; j < i; j++) ret += rel[s[i] - 'a' + 1][s[j] - 'a' + 1];
		}
		write(ret), putchar('\n');
	}

我知道你们想看什么——AC Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
template<class T>
void write(T x){
    if(x < 0)putchar('-'),x = -x;
    if(x > 9)write(x / 10);
    putchar(x % 10 + '0');
}
template<class T>
inline T read(){
    T x = 0, f = 1;char ch = getchar();
    while(ch < '0'||ch > '9'){if(ch == '-') f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
    return x * f;
}
template<class T> inline T read(T &x){ return x = read<ll>();}
int n, q;
const int N = 2e6 + 100;
ll trie[N][37], cnt = 0, sm[N], rel[37][37];
void insert(string s){
	int p = 0;
	for(auto c : s){
		int u = c - 'a' + 1;
		if(!trie[p][u]) trie[p][u] = ++cnt;
		for(int j = 0; j <= 26; j++){
			if(j == u)continue;
			rel[j][u] += sm[trie[p][j]];
		}
		sm[p = trie[p][u]] ++;
	}
}
int main(){
	read(n), read(q);
	for(int i = 1; i <= n; i++){
		string s; cin >> s;
		s += 'a' - 1; insert(s);
	}
	while(q--){
		string s; cin >> s;
		ll ret = 0;
		for(int i = 0; i < 26; i++){
			ret += rel[s[i] - 'a' + 1][0];
			for(int j = 0; j < i; j++) ret += rel[s[i] - 'a' + 1][s[j] - 'a' + 1];
		}
		write(ret), putchar('\n');
	}
}